Сэмплинг: несколько важных правил
Содержание:
Сэмплинг акции
Прежде чем проводить сэмплинг-акцию стоит взвесить все преимущества и недостатки метода. Главное, определить какая конкретно задача стоит в конкретном случае: повысить объем продаж, продвижение нового неизвестного пока продукта, повысить известность товарной марки или что-то еще.
Проведение сэмплинга задача дорогостоящая, поэтому стоит просчитать все заранее. Здесь надо учесть стоимость наладки производства для изготовления пробников, оплата персонала, стоимость аккредитации.
Кроме того, могут потребоваться расходы на специальную одежду для промоутеров.
Акцию можно проводить своими силами — это значит самим набирать персонал, договариваться о разрешении проведения акции в предполагаемом месте.
Или можно переложить эту ответственность на специализированные фирмы и только оплатить расходы. Если планируется крупномасштабная акция с участием нескольких городов или точек, то предпочтительнее привлечь профессионалов.
Стратегии сэмплирования[править]
- Cубдискретизация (англ. under-sampling) — удаление некоторого количества примеров мажоритарного класса.
- Передискретизации (англ. over-sampling) — увеличение количества примеров миноритарного класса.
- Комбинирование (англ. сombining over- and under-sampling) — последовательное применение субдискретизации и передискретизации.
- Ансамбль сбалансированных наборов (англ. ensemble balanced sets) — использование встроенных методов сэмплирования в процессе построения ансамблей классификаторов.
Также все методы можно разделить на две группы: случайные (недетерминированные) и специальные (детерминированные).
- Случайное сэмплирование (англ. random sampling) — для этого типа сэмплирования существует равная вероятность выбора любого конкретного элемента. Например, выбор 10 чисел в промежутке от 1 до 100. Здесь каждое число имеет равную вероятность быть выбранным.
- Сэплирование с заменой (англ. sampling with replacement) — здесь элемент, который выбирается первым, не должен влиять на вторую или любую другую выборку. Математически, ковариация равна нулю между двумя выборками. Мы должны использовать выборку с заменой, когда у нас большой набор данных. Потому что, если мы используем выборку без замены, то вероятность для каждого предмета, который будет выбран, будет изменяться, и она будет слишком сложной после определенного момента. Выборка с заменой может сказать нам, что чаще встречается в наших данных.
- Сэмплирование без замены (англ. sampling without replacement) — здесь то, что мы выбираем первым, повлияет на второе. Выборка без замены полезна, если набор данных мал. Математически, ковариация между двумя выборками не равна нулю.
- Стратифицированное сэмплирование (англ. stratified sampling) — в этом типе техники мы выбираем из определенной группы объектов из всей выборки. Из каждой группы извлекается одинаковое количество объектов, хотя группы имеют разные размеры. Кроме того, существует вариант, когда количество объектов, выбранных из каждой группы, пропорционально размеру этой группы.
Какие инструменты использовать?
Пожалуй, можно выделить три основные группы приемов, относящихся к категории «семплинг»:
Раздача бесплатных образцов продукции
Таким образом, можно познакомить покупателя с новым брендом, товаром, его свойствами и преимуществами. Согласно статистике покупатель склонен доверять проверенным компаниям и покупать уже протестированную на личном опыте продукцию. Но в том случае, когда предоставляет возможность лично убедиться в уникальных свойствах и качествах нового товара, причем это необязательно делать в торговой точке, а можно унести продукт домой, то интерес потребительской аудитории возрастает в несколько раз. Самый видимый эффект этот прием оказывает при первичном запуске товара на рынке или при повторной рекламной кампании, но с акцентом на измененные свойства товара. Раздача бесплатных образцов продукции довольно активно применяется участниками рынка, так как имеет видимый результат в качестве повышения уровня спроса на продвигаемый товар.
Раздача рекламных материалов с прикрепленным пробником продукции
Как правило, подобные акции проходят не только в местах продаж, но и на открытых пространствах (улицах, массовых мероприятиях, на территории торгово-развлекательных центров). Сама механика раздачи печатной продукции не так эффективна, как в тандеме с сэмплингом. Таким образом, у потенциального потребителя появляется возможность не только узнать полезную информацию о продукте, но и протестировать (попробовать) пробный экземпляр в действии. Например, это может быть реклама нового чая с помощью информационной листовки с прикрепленным к нему образцом продукции или продвижение обновленной линейки известного косметического бренда в виде буклета с сэмплом крема для лица.
Комплекс мероприятий
Если смотреть на сэмплинг как механику btl активности в широком спектре, то к проектам подобного рода можно отнести все мероприятия, в той или иной мере знакомящие покупателей товаров (дегустация, тест-драйв, спреинг и т.д). К примеру, производитель круп или макарон вполне может организовать дегустацию своей продукции в торговой точке, а в качестве дополнительного стимула для покупки товара вручать бесплатный образец продукции (на одну порцию).
Конечно, использование того или иного инструмента должно быть аргументировано, продумано и качественно организовано, только в этом случае можно говорить о положительном и эффективном результате. Однако в руках профессионалов сэмплинг как прием маркетинга может заиграть совсем новым красками, ведь никто не запрещает экспериментировать, совмещать сразу несколько техник в одном проекте. Главное, не забывать один из главных принципов маркетинга: «Не будьте занудой!»
Calculating Power Spectral Density¶
Last chapter we learned that we can convert a signal to the frequency domain using an FFT, and the result is called the Power Spectral Density (PSD).
But to actually find the PSD of a batch of samples and plot it, we do more than just take an FFT.
We must do the following six operations to calculate PSD:
- Take the FFT of our samples. If we have x samples, the FFT size will be the length of x by default. Let’s use the first 1,024 samples as an example to create a 1,024-size FFT. The output will be 1,024 complex floats.
- Take the magnitude of the FFT output, which provides us 1,024 real floats.
- Normalize: divide by the FFT size (, or 1,024 in this case).
- Square the resulting magnitude to get power.
- Convert to dB using ; we always view PSDs in log scale.
- Perform an FFT shift, covered in the previous chapter, to move “0 Hz” in the center and negative frequencies to the left of center.
Those six steps in Python are:
Fs = 1e6 # lets say we sampled at 1 MHz # assume x contains your array of IQ samples N = 1024 x = xN # we will only take the FFT of the first 1024 samples, see text below PSD = (np.abs(np.fft.fft(x))N)**2 PSD_log = 10.0*np.log10(PSD) PSD_shifted = np.fft.fftshift(PSD_log)
Optionally we can apply a window, like we learned about in the chapter. Windowing would occur right before the line of code with fft().
# add the following line after doing x = x x = x * np.hamming(len(x)) # apply a Hamming window
To plot this PSD we need to know the values of the x-axis.
As we learned last chapter, when we sample a signal, we only “see” the spectrum between -Fs/2 and Fs/2 where Fs is our sample rate.
The resolution we achieve in the frequency domain depends on the size of our FFT, which by default is equal to the number of samples on which we perform the FFT operation.
In this case our x-axis is 1,024 equally spaced points between -0.5 MHz and 0.5 MHz.
If we had tuned our SDR to 2.4 GHz, our observation window would be between 2.3995 GHz and 2.4005 GHz.
In Python, shifting the observation window will look like:
center_freq = 2.4e9 # frequency we tuned our SDR to f = np.arange(Fs/-2.0, Fs2.0, FsN) # start, stop, step. centered around 0 Hz f += center_freq # now add center frequency plt.plot(f, PSD_shifted) plt.show()
We should be left with a beautiful PSD!
If you want to find the PSD of millions of samples, don’t do a million-point FFT because it will probably take forever. It will give you an output of a million “frequency bins”, after all, which is too much to show in a plot.
Instead I suggest doing multiple smaller PSDs and averaging them together or displaying them using a spectrogram plot.
Alternatively, if you know your signal is not changing fast, it’s adequate to use a few thousand samples and find the PSD of those; within that time-frame of a few thousand samples you will likely capture enough of the signal to get a nice representation.
Here is a full code example that includes generating a signal (complex exponential at 50 Hz) and noise. Note that N, the number of samples to simulate, becomes the FFT length because we take the FFT of the entire simulated signal.
import numpy as np
import matplotlib.pyplot as plt
Fs = 300 # sample rate
Ts = 1Fs # sample period
N = 2048 # number of samples to simulate
t = Ts*np.arange(N)
x = np.exp(1j*2*np.pi*50*t) # simulates sinusoid at 50 Hz
n = (np.random.randn(N) + 1j*np.random.randn(N))np.sqrt(2) # complex noise with unity power
noise_power = 2
r = x + n * np.sqrt(noise_power)
PSD = (np.abs(np.fft.fft(r))N)**2
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)
f = np.arange(Fs/-2.0, Fs2.0, FsN) # start, stop, step
plt.plot(f, PSD_shifted)
plt.xlabel("Frequency ")
plt.ylabel("Magnitude ")
plt.grid(True)
plt.show()
Output:
Sampling Distribution — Central Limit Theorem
The outcome of our simulation shows a very interesting phenomenon: the sampling distribution of sample means is very different from the of marriages over 976 inhabitants: the sampling distribution is much less skewed (or more symmetrical) and smoother.
In fact, means and sums are always (approximately) for reasonable sample sizes, say n > 30. This doesn’t depend on whatever population distribution the data values may or may not follow. This phenomenon is known as the central limit theorem.
Note that even for 1,000 samples of n = 10, our sampling distribution of means is already looking somewhat similar to the normal distribution shown below.
Sampling and non-sampling errors: 5 examples
1. Population specification error (non-sampling error)
This error occurs when the researcher does not understand who they should survey. For example, imagine a survey about breakfast cereal consumption in families. Who to survey? It might be the entire family, the person who most often does the grocery shopping, or the children. The shopper might make the purchase decision, but the children influence the cereal choice.
This kind of non-sampling error can be avoided by thoroughly understanding your research question before you begin constructing a questionnaire or selecting respondents.
2. Sample frame error (non-sampling error)
A frame error occurs when the wrong sub-population is used to select a sample. A classic frame error occurred in the 1936 presidential election between Roosevelt and Landon. The sample frame was from car registrations and telephone directories. In 1936, many Americans did not own cars or telephones, and those who did were largely Republicans. The results wrongly predicted a Republican victory.
The error here lies in the way a sample has been selected. Bias has been unconsciously introduced because the researchers didn’t anticipate that only certain kinds of people would show up in their list of respondents, and parts of the population of interest have been excluded. A modern equivalent might be using cell phone numbers, and therefore inadvertently missing out on adults who don’t own a cell phone, such as older people or those with severe learning disabilities.
Frame errors can also happen when respondents from outside the population of interest are incorrectly included. For example, say a researcher is doing a national study. Their list might be drawn from a geographical map area that accidentally includes a small corner of a foreign territory – and therefore include respondents who are not relevant to the scope of the study.
3. Selection error (non-sampling error)
This occurs when respondents self-select their participation in the study – only those that are interested respond. It can also be introduced from the researcher’s side as a non-random sampling error. For example, if a researcher puts out a call for responses on social media, they’re going to get responses from people they know, and of those people, only the more helpful or affable individuals will reply.
Selection error can be controlled by going extra lengths to get participation. A typical survey process includes initiating pre-survey contact requesting cooperation, actual surveying, and post-survey follow-up. If a response is not received, a second survey request follows, and perhaps interviews using alternate modes such as telephone or person-to-person.
4. Non-response (non-sampling error)
Non-response errors occur when respondents are different than those who do not respond. For example, say you’re a company doing market research in advance of launching a new product. You might get a disproportionate level of participation from your existing customers, since they know who you are, and miss out on hearing from a broader pool of people who don’t yet buy from you.
This may occur because either the potential respondent was not contacted or they refused to respond. The extent of this non-response error can be checked through follow-up surveys using alternate modes.
5. Sampling errors
As described previously, sampling errors occur because of variation in the number or representativeness of the sample that responds. Sampling errors can be controlled and reduced by (1) careful sample designs, (2) large enough samples (check out our online sample size calculator), and (3) multiple contacts to assure a representative response.
Be sure to keep an eye out for these sampling and non-sampling errors so you can avoid them in your research.
Steps involved in Sampling
I firmly believe visualizing a concept is a great way to ingrain it in your mind. So here’s a step-by-step process of how sampling is typically done, in flowchart form!
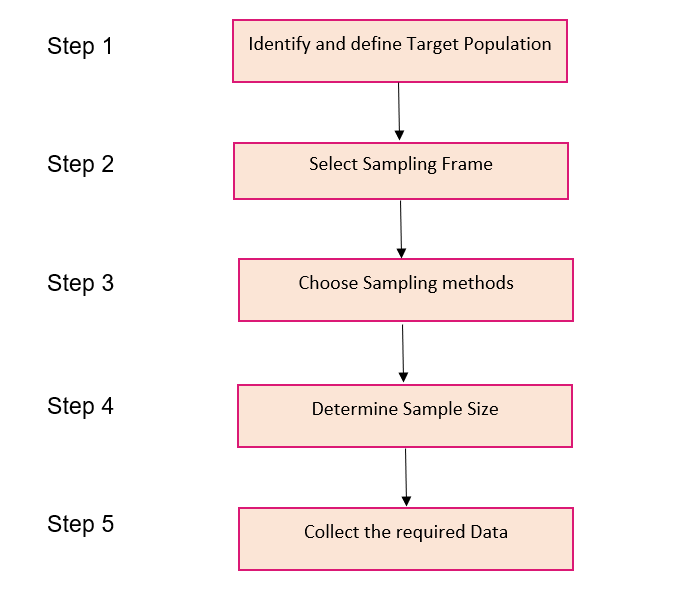
Let’s take an interesting case study and apply these steps to perform sampling. We recently conducted General Elections in India a few months back. You must have seen the public opinion polls every news channel was running at the time:

Were these results concluded by considering the views of all 900 million voters of the country or a fraction of these voters? Let us see how it was done.
Step 1
So, to carry out opinion polls, polling agencies consider only the people who are above 18 years of age and are eligible to vote in the population.
Step 2
Sampling Frame – It is a list of items or people forming a population from which the sample is taken.
So, the sampling frame would be the list of all the people whose names appear on the voter list of a constituency.
Step 3
Generally, probability sampling methods are used because every vote has equal value and any person can be included in the sample irrespective of his caste, community, or religion. Different samples are taken from different regions all over the country.
Step 4
Sample Size – It is the number of individuals or items to be taken in a sample that would be enough to make inferences about the population with the desired level of accuracy and precision.
Larger the sample size, more accurate our inference about the population would be.
For the polls, agencies try to get as many people as possible of diverse backgrounds to be included in the sample as it would help in predicting the number of seats a political party can win.
Step 5
Once the target population, sampling frame, sampling technique, and sample size have been established, the next step is to collect data from the sample.
In opinion polls, agencies generally put questions to the people, like which political party are they going to vote for or has the previous party done any work, etc.
Based on the answers, agencies try to interpret who the people of a constituency are going to vote for and approximately how many seats is a political party going to win. Pretty exciting work, right?!
Пример (задача о моллюсках)
Сравним практически некоторые из описанных стратегий на наборе данных про моллюсков (набор данных взят с UCI machine learning repository). В нем представлены физиологические сведения об этих животных. Имеются следующие поля:
- пол;
- длина;
- диаметр (линия, перпендикулярная длине);
- высота;
- масса всего моллюска;
- масса без раковины;
- масса всех внутренних органов (после обескровливания);
- масса раковины (после высушивания);
- зависимая переменная: количество колец (в год на раковине моллюска появляется 1,5 кольца).
Изначально набор данных предназначен для решения задачи регрессии. По количеству колец на раковине определяется возраст моллюска. Для классификации в условиях несбалансированности создадим новую выходную переменную, принимающую только два значения. Для этого, предположим, что если количество колец у моллюска не превосходит 18, то для нас он будет считаться молодым, в противном случае – старым.
Также проимитируем ситуацию различия издержек и рассмотрим случаи, когда неверное отнесение старого моллюска к молодым может принести бо́льшие издержки, чем в случае неверной классификации фактически молодого.
Таким образом, мы получили набор данных с сильно несбалансированными классами, где значение «молодой» было присвоено 4083 записям (97,7%), а значение «старый» – 94 записям (2,3%). Далее стратифицированным сэмплингом были получены тестовый и обучающий наборы данных.
Прежде чем восстанавливать баланс между классами, вернемся к понятию издержек классификации. Во многих приложениях, таких как кредитный скоринг, директ-маркетинг, издержки при ложноположительной ($С_{10}$) классификации в несколько раз выше, чем при ложноотрицательной (обозначим их как $С_{01}$). При пороге отсечения 0,5 количество миноритарных примеров необходимо увеличить в $С_{10}/С_{01}$ раз (при условии что $С_{00} = С_{11} = 0$). Либо во столько же уменьшить мажоритарный класс (теоретическое обоснование этого утверждения изложено в работе ).
Сравним следующие подходы к восстановлению баланса между классами: случайное удаление примеров мажоритарного класса, дублирование примеров миноритарного класса, специальные методы увеличения числа примеров (алгоритмы SMOTE и ASMO).
Для алгоритмов SMOTE и ASMO количество ближайших соседей для генерации примеров установим равным 5.
Алгоритм ASMO признал набор данных нерассеянным (среди 100 ближайших соседей не нашлось даже 20 примеров из мажоритарного класса). Однако проигнорируем это сообщение и посмотрим, какой будет результат, если генерировать примеры, используя записи из каждого класса. Для кластеризации применен алгоритм k-means (k = 5).
После восстановления баланса строилась логистическая регрессия с порогом отсечения 0,5, и подсчитывались издержки. Результаты представлены на рисунке 7.
Из рисунка 6 видно, что наилучшим образом показал себя алгоритм SMOTE, так как издержки в данном случае оказались самыми меньшими. ASMO проявил себя хуже, однако стоит напомнить, что набор данных не рассеян и согласно данной стратегии необходимо было использовать SMOTE.
Итак, мы рассмотрели различные подходы сэмплинга для решения проблемы несбалансированности классов. Помимо него существуют стратегии, согласно которым происходит модификация алгоритма обучения, но их рассмотрение выходит за рамки данной статьи.
В таблице 1 приведено описание файлов с наборами данных, которые использовались в примере. Их можно найти в архиве.
Таблица 1 – Наборы данных
| Описание набора данных | Файл |
|---|---|
| Исходный набор данных: Abalone Data Set (классы не выделены) | abalone_data.txt |
| Исходный обучающий набор данных | dataset75.txt |
| Тестовый набор данных | testdataset.txt |
| Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:3 | syntsmote1_3.txt |
| Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:5 | syntsmote1_5.txt |
| Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:10 | syntsmote1_10.txt |
| Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:15 | syntsmote1_15.txt |
| Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:3 | syntasmot1_3.txt |
| Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:5 | syntasmot1_5.txt |
| Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:10 | syntasmot1_10.txt |
| Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:15 | syntasmot1_15.txt |
When sampling is applied
The following sections explain where you can expect session sampling in Analytics reports.
Default reports
Analytics has a set of preconfigured, default reports listed in the left pane under Audience, Acquisition, Behavior, and Conversions.
Analytics stores one complete, unfiltered set of data for each property in each account. For each reporting view in a property, Analytics also creates tables of aggregated dimensions and metrics from the complete, unfiltered data. When you run a default report, Analytics queries the tables of aggregated data to quickly deliver unsampled results.
Analytics periodically adds new reports, and sometimes makes changes to the way metrics are calculated. If the date range of a report includes a time before the report was added or before a metric calculation changed, then Analytics can issue an ad-hoc query, and the data might be sampled.
Data is sampled when reports that include the Users and Active Users metrics include data from before September 2016. Learn more
Default reports are unsampled in both Analytics Standard and Analytics 360. However, if you use the , you may experience sampling in some of your Google Ads reports.
Ad-hoc reports
If you modify a default report in some way—for example, by applying a segment, filter, or secondary dimension—or if you create a custom report with a combination of dimensions and metrics that don’t exist in a default report, you are generating an ad-hoc query of Analytics data.
Analytics first goes to the aggregated data tables to see if all of the requested information from your ad-hoc query is available there. If the information is not available there, Analytics queries the complete, unfiltered set of data to satisfy the query request.
Ad-hoc queries are subject to sampling if the number of sessions for the date range you are using exceeds the threshold for your property type.
The sampling algorithm uses a sample of the complete data that is proportional to the daily distribution of sessions for the property for the date range you’re using. For example, if over a 5-day period, sessions were sampled at 25%, then the sample would include 25% of each day’s sessions:
| Monday | Tuesday | Wednesday | Thursday | Friday | |
|---|---|---|---|---|---|
| Total sessions | 200,000 | 100,000 | 200,000 | 300,000 | 200,000 |
| 25% sample | 50,000 | 25,000 | 50,000 | 75,000 | 50,000 |
The sampling rate varies from query to query depending on the number of sessions during a date range for a given view.
When sampling is in effect, you see a message at the top of the report that says This report is based on N% of sessions.
To the right of that message, you can select one of two options to change the sampling size:
- Greater precision: Uses the maximum sample size possible to give you results that are the most precise representation of your full data set
- Faster response: Uses a smaller sampling size to give you faster results
Sampling controls.
Other reports
Sampling works differently for these reports than for default reports or ad-hoc queries.
Multi-Channel Funnels reports
Like default reports, no sampling is applied unless you modify the report—for example, by changing the lookback window, by changing which conversions are included, or by adding a segment or secondary dimension. If you modify the report in any way, a maximum sample of 1M conversions will be returned.
Flow-visualization reports
Flow-visualization reports (Users Flow, Behavior Flow, Events Flow, Goal Flow) are generated from a maximum of 100K sessions for the selected date range.
The flow-visualization reports, including entrance, exit, and conversion rates, may differ from the results in the default Behavior and Conversions reports, which are based on a different sample set.
Filters and segments
Analytics Standard and Analytics 360 sample session data at the view level, after view filters have been applied. For example, if view filters include or exclude sessions, then the sample is taken from only those sessions.
Analytics Standard and Analytics 360 both apply segments after applying report filters and after sampling, which means that a segment may include fewer sessions than are included in the overall sample.