Пример построения сетевого графика

Метод сетевой модели номер два

Вторым методом сетевого планирования, по праву завоевавшим популярность среди проект-менеджеров, является диаграмма, называемая «вершина – работа». В англоязычной версии модель сокращенно обозначается как AoN (Activity on Node). Метод отличается большей простой и наглядностью, предлагает узлами модели делать не события, а работы. При этом длина прямоугольников, обозначающих операции, может указывать на их длительность во времени. Отношения предшествования между ними оформляются прямыми или фигурными стрелками.

Такую диаграмму сформировать значительно проще, чем AoA. Тем не менее, алгоритм работы над ней очень похож. События на диаграмме не размещаются, но они предполагаются в завершении каждой работы. Помимо прочего, событиям все-таки уготовано место на сетевом графике, но в форме особых фактов, именуемых вехами. Веха – это особенное значимое событие проекта, и не каждая операция должна ею завершаться. Поэтому диаграмма может быть разгружена от несущественных событий, но отражать важные, ключевые моменты проектной реализации.

Пример сетевой диаграммы метода «вершина – работа»

Если воспользоваться возможностью вариации длины прямоугольников работ, превращая их в ленты, размер которых соответствует длительности реализации, то сетевой график превращается в диаграмму Ганта. Диаграмма вида AoN при этом становится похожей на АоА. В методе AoN отпадает необходимость в изображении фиктивных работ, требуемых в модели «ребро – работа» для своеобразной «упаковки» событий. Благодаря этому лишние, искусственные сущности исключаются из поля зрения менеджера проекта. Вехи в этом отношении являются более интересным решением, располагаясь, как и все работы, в узлах сетевого графика.

Работы перестают выполнять двойную функцию связующих события элементов и непосредственного обозначения выполняемых операций. Для метода AoN не требуется нумерации, что дает PM мобильность для свободного маневрирования числом мероприятий. И в этом кроется еще одно удобство метода «вершина – работа». В сетевой диаграмме должны быть учтены возможности применения различных связей предшествования. Их количество не столь велико, как может показаться на первый взгляд. Оно связано с вариантом связи предшествования и с эффектом отставания или опережения в отношении к примененной типовой связи. Все это мы рассмотрим в отдельном материале, посвященном практике сетевого планирования и управления.

В настоящей статье мы рассмотрели методы сетевого планирования и управления. В современной проектной практике отдается предпочтение методу AoN как более доступному и наглядному. Это не означает, что метод АоА плох, многие специалисты, освоив его, с успехом применяют. Обе модели приводят к одному и тому же результату, но с двух взаимосвязанных сторон: работ и событий. Проект-менеджер должен понимать суть и уметь применять каждый из представленных инструментов. Это связано с тем, что задача сетевого планирования состоит в поиске наиболее экономичных, ясных решений построения событийной и временной последовательности в условиях ограничений.

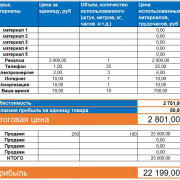
Минимизация числа исполнителей проекта при сохранении времени его выполнения

линейная диаграммакарта проекта

• минимизировать количество одновременно занятых исполнителей;
• выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.

• перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
• работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
• работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
• перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
• передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.

калькулятора

Таблица 1

Работа (ij)	Длительность t(ij), дн.	Количество исполнителей
1,2	4	5
2,3	6	3
2,4	5	6
2,7	11	6
3,5	9	1
4,6	9	2
5,7	11	3
6,7	10	5
7,8	4	6

Рис. 1. Пример сетевого графика

Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.

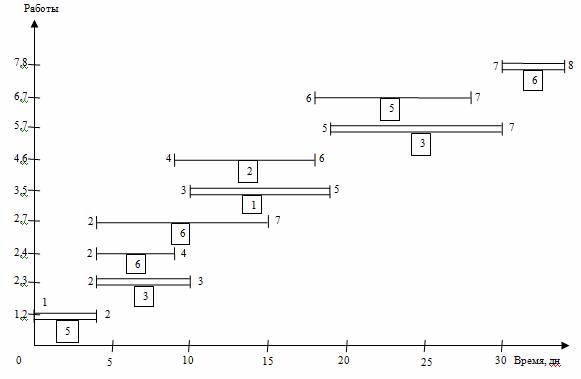
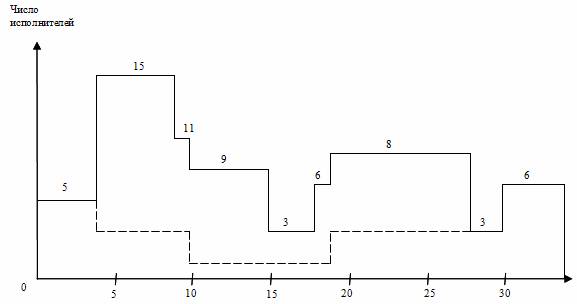Рис. 2. Линейная диаграмма и карта проекта до оптимизации

15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.

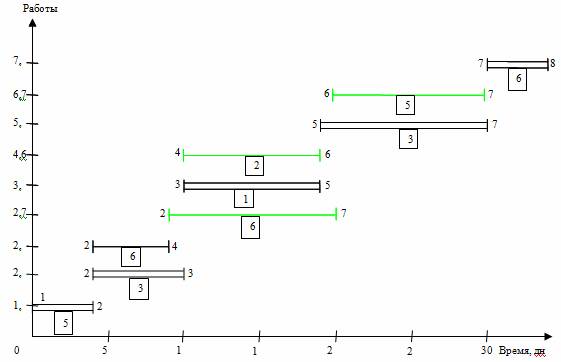
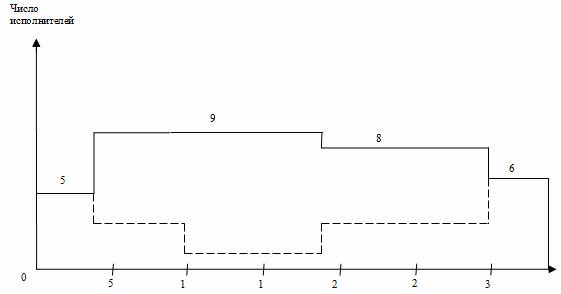
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено.

Видеоинструкция

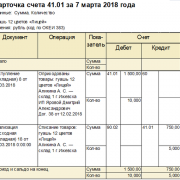
Построение сетевой диаграммы

После структуризации операций осуществляется первичное планирование и построение сетевой модели в соответствии с запланированными операциями. Для этого составляется формуляр операций в виде таблицы, в которой содержатся следующие данные:

• последовательный перечень всех операций, которые должны быть выполнены в рамках проекта или плана действий на заданный период;
• по каждой операции должна быть указана ее продолжительность и количество исполнителей, которые задействованы в ее реализации;
• каждой операции, кроме начальной, должны соответствовать предшествующие операции.

Пример таблицы операций по проекту проведения конкурса на выбор лучшей школы города приведен в таблице.

Пример таблицы операций

№	Наименование операции	Предыдущие операции	Продолжи-тельность, дни	Кол-во исполнителей, чел.
1	Подписание распоряжения о проведении конкурса	—	1	1
2	Регистрация школ	1	4	2
3	Поиск помещения для проведения конкурса	1	2	2
4	Отбор персонала для проведения конкурса	1	1	3
5	Подготовка помещения	2, 3	1	1
6	Разработка плана проведения конкурса	2 (1)	8	2
7	Инструктаж персонала	4	1	2
8	Обустройство помещения перед проведением конкурса	5	4	2
9	Проведение конкурса	6, 8	1	3
10	Подведение итогов конкурса	7, 9	1	3

В соответствии с формализованной структурой операций и таблицы операций необходимо осуществить построение сетевой модели.

Воспользуемся данными по операциям из таблицы и представим сетевую диаграмму данных работ.

Пример построения сетевой диаграммы

В данной сетевой модели вершина представляет собой конкретную операцию, а линии – взаимосвязь между ними. В данной диаграмме в каждой вершине верхняя цифра обозначает номер операции, нижняя указывает на продолжительность данной операции в днях, неделях или иных единицах. Данный подход также называется построением диаграммы предшествования и следования и является наиболее распространенным представлением сетевых моделей в планировании.

Построение сетевых моделей по типу «вершина-работа» наиболее распространено в практике управления и активно применяется в сфере государственного и муниципального управления, в планировании на промышленных, производственных и коммерческих предприятиях различных отраслей экономики.

Далее необходимо определить критический путь.

Критический путь, как видно из рисунка, составляют следующие операции: 1, 2, 6, 9 и 10.

Следовательно, длина критического пути составляет:

1+4+8+1+1=15 дней.

По результатам планирования и построения сетевой модели можно сделать один из двух выводов:

1. В случае, если сетевая модель и длина критического пути свидетельствуют о том, что вся совокупность операций по продолжительности укладывается в заданный срок, то считается, что реализация проекта или заданного плана действий будет произведена корректно.
2. В случае, если деятельность по реализации проекта или заданного плана действий не укладывается в отведенный для этого срок, производится корректировка сетевой модели.

Как выглядит график

Любой привычный нам график представлен кривой, расположенной на плоскости (реже в пространстве). Но вид сетевого плана существенно отличается.

Сетевой график проекта может выглядеть двояко: одна методика предполагает обозначение операций в узлах блок-схемы (ОУ), вторая использует для этого соединительные стрелки (ОС). Гораздо удобнее использовать первый способ.

Операция обозначается круглым или прямоугольным блоком. Стрелки, их соединяющие, определяют взаимосвязи между действиями. Поскольку названия работ могут быть достаточно длинными и объемными, в блоках проставляют номера операций, а к графику составляется спецификация.

Построение сетевого графика

В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.

В таблицу сведем следующие данные по каждой операции:

• номер операции;
• предшествующие операции;
• количество исполнителей;
• продолжительность операции в днях.

В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.

Таблица операций для построения сетевого графика

Номер операции	Предыдущие операции	Кол-во исполнителей, чел.	Продолжительность, дни
1.	—	10	1
2.	1	2	3
3.	1	3	1
4.	1	2	4
5.	4	1	0,5
6.	3	3	2
7.	5	2	0,5
8.	2,7,6	10	0,5
9.	9	10	0,5
10.	9	1	3
11.	9	2	4
12.	9	2	2
13.	9	2	3
14.	12	2	2
15.	13	3	2
16.	10,11,14,15	10	0,5
17.	16	10	0,5
18.	17	2	2
19.	18	2	3
20.	17	2	2
21.	17	2	3
22.	21	3	1
23.	20	2	2
24.	19,22,23	10	0,5
25.	24	10	0,5
26.	25	5	1
27.	26	5	3
28.	25	3	2
29.	28	3	2
30.	25	2	4
31.	27,29,30	10	0,5
32.	31	10	0,5
33.	32	7	1
34.	32	2	1
35.	33,34	10	1

На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.

Сетевой график, пример

Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.

В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.

Для соблюдения запланированных сроков произведем корректировку сетевого графика.

В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.

После корректировки осуществим построение альтернативного сетевого графика.

Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:

Q = N * t

Q4 = 2*4 = 8 ч/дн

Q13 = 2*3 = 6 ч/дн

Q18 = 2*2 = 4 ч/дн

В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.

В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.

В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.

В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:

26 – 2 – 1 – 1 = 22 дня.

Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.

Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.

Альтернативный сетевой график

Предварительный этап построения сетевого графика

На предварительном этапе сетевого планирования необходимо определить характер планируемых операций и потенциал сотрудников, которые будут отвечать за их выполнение.

В качестве примера возьмем работу регионального Агентства по молодежной политике на месяц и запланируем перечень операций на месяц.

Допустим, что количество сотрудников – 10 человек.

Типовая оргструктура Агентства по молодежной политике

Построение сетевого графика представляет собой элемент управленческой деятельности и соответствует общему процессу принятия решений. Это неотъемлемая составляющая процесса управления. В ходе построения сетевого графика рассматриваются несколько вариантов выполнения запланированных операций и в итоге выбирается наилучшая альтернатива из множества доступных. В сетевой график включаются непосредственно управленческие действия и операции, связанные с технической стороной деятельности организации.

Управленческие и технические операции в сетевом графике

Управленческие операции	Технические операции
Общее управление внутренними процессами в организации	Непосредственное проведение запланированных операций
Проектирование системы управления	Подведение итогов
Стратегическое планирование	Работа с документами, регистрами
Управленческое консультирование	Оценка результатов
Управление сотрудниками	Оформление документации
Взаимодействие с внешней средой	Формализация результатов

Операции в сетевом графике должны быть зафиксированы документально, например, в распорядительных документах. Основное назначение такой документации состоит в регулировании деятельности объекта управления, обеспечении его финансовыми, трудовыми, материальными и информационными ресурсами. Основные формы документального представления запланированных операций:

1. Приказы – в том числе распоряжения, указания;
2. Акты – в том числе акцепты и протоколы;
3. Договоры – в том числе, соглашения, контракты, оферты;
4. Регламенты – инструкции, положения, правила, планы, модели.

Цель и задачи сетевого планирования

Основное назначение методологии сетевого планирования в управлении сократить до минимума продолжительность проекта. С помощью сетевых моделей руководитель может системно оценивать текущий и перспективный ход запланированных операций, за счет чего возможно управление процессом реализации проекта в целом. Календарно-сетевое планирование позволяет также рационально оперировать имеющимися в распоряжении ресурсами.

Основная цель сетевого планирования следует из его назначения: построить модель реализации проекта на основе формирования комплекса работ, задания их очередности, определить необходимые ресурсы и задачи, которые должны быть решены для завершения проекта. В итоге необходимо добиться сокращения до минимума продолжительности проекта.

Метод сетевого планирования позволяет координировать деятельность участников проекта, определить порядок, согласно которому должны выполняться запланированные работы, операции, действия. При этом основу составляет продолжительность каждой операции, действия, которые должны быть определены с учетом потребностей в материальных, трудовых и финансовых ресурсах.

Применение методологии сетевого планирования в управлении предполагает формализацию структуры операций в информационно-табличном виде, на основе чего осуществляется структуризация операций по отрезкам времени и группировка параллельных операций для оптимального выполнения всего проекта в целом. На основе этого осуществляется построение таблицы операций, в которую сводятся все значимые данные по каждой операции в соответствии с формализованной структурой операций и группами параллельных операций. Результатом является построение сетевой диаграммы, которая подлежит корректировке в случае несоответствия запланированных действий общему сроку их выполнения, либо отдельным промежуткам времени внутри общей временной структуры проекта.

Задачи сетевого планирования:

1. Определить перечень критических работ или операций (т.е. таких операций, которые имеют наибольшее влияние на общую продолжительность проекта);
2. Построить сетевой план проекта таким образом, чтобы все запланированные работы и операции были произведены с соблюдением заданных сроков и минимальных затратах.

Единица такой сетевой модели – операция (работа или задача), которая означает какую-либо деятельность, в результате выполнения которой будут достигнуты определенные результаты.

Результатом сетевого планирования является графическое отображение последовательности операций, выполнение которых приведет к достижению конечной цели проекта. Основным способом отображения являются сетевые экономико-математические модели. Для управленческой деятельности наиболее подходят сетевые графики. С помощью сетевой модели формируется возможность системного представления всех операций и условия для управления процессом осуществления проекта. При необходимости метод сетевого планирования позволяет маневрировать ресурсами в рамках модели для достижения конечной цели.

Сетевое планирование позволяет исключить влияние субъективных факторов на управление проектом, способствуя сокращению сроков реализации проекта минимум на 15-20%, рационализации использования имеющихся ресурсов и оптимизации затрат. При этом отдельные операции рассматриваются как отдельные элементы целостной системы, а исполнители выступают звеньями данной системы.

Варианты связей и отношение предшествования

Сетевые методы планирования строятся по моделям, в которых проект представляется как целостная совокупность взаимосвязанных работ. Данные модели во многом формируются типом и видом связей между операциями реализации проекта. С позиции типа различаются жесткие, мягкие и ресурсные связи. Видовое различие взаимосвязанности операций основано на отношения предшествования. Рассмотрим основные типы связи.

Мягкие связи. Им соответствует особая, «дискреционная» логика, дающая «мягкую» основу для выбора операций к размещению на диаграмму, диктуемого технологией. В то время как технология длительный период развивалась на протяжении многих циклов, вырабатываются правила делового оборота, не требующие дополнительной фиксации и планирования. Это экономит время, место модели, стоимость и не требует дополнительного контроля со стороны PM. Поэтому менеджер проекта сам решает, нужна ему такая выделенная операция, или нет.
Жесткие связи. Данный вид связей основан на технологической логике. Они предписывают выполнение конкретных действий строго после других, что сообразно с процессуальной логикой. Например, наладку оборудования можно осуществлять только после его монтажа. Тестирование недочетов технологии допустимо проводить, если сдача ее в опытную эксплуатацию произошла и т.д

Иными словами, принятая технология (неважно, в какой сфере она реализуется) жестко навязывает последовательность мероприятий и событий проекта, что и обуславливает соответствующий тип связи.
Ресурсные связи. В условиях назначения на один ответственный ресурс нескольких задач возникает его перегруженность, что может привести к удорожанию проекта

За счет подведения под менее критичную задачу дополнительного ресурса этого можно избежать, и такие связи называются ресурсными.

В момент формирования расписания проекта сначала применяются жесткие, а затем – мягкие связи. Далее, по необходимости, некоторые мягкие связи подлежат сокращению. Благодаря этому может быть достигнуто некоторое сокращение общей длительности проекта. В условиях перегруженности некоторых ответственных ресурсов из-за параллельных работ допустимо разрешение возникших конфликтов введением ресурсных связей. Однако следует контролировать, чтобы новые связи не привели к значительным изменениям общего плана.

Сопряженные работы как некая последовательность проектной задачи связаны друг с другом. Назовем их операциями А и В. Введем понятие отношения предшествования, которое рассматривается как некое ограничение на сроки и общую продолжительность, так как операция В не может начаться до момента окончания операции А. Это означает, что В и А связаны отношением простого предшествования, при этом вовсе не обязательно, чтобы В начиналось одномоментно с окончанием А. Например, отделочные работы начинаются после возведения крыши дома, но это не означает, что выполняться они должны в тот же момент, когда наступит указанное событие.

Инструкция к сервису

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с , для этого нужно снять отметку с пункта Нумерация вершин с №1.

12341103015
Нумерация вершин с 0
1231103015

Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить.
Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции.

docxpngMicrosoft Visioduration, ES, EF, LS, LF, and slack

Масштабный сетевой график

1. Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
2. Построить масштабный сетевой график.
3. Оценить вероятность выполнения всего комплекса работ за 30 дней.
4. Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.

Код работы ( i,j)	Продолжительность
tmin (i,j)	tmax (i,j)
1,2	5	10
1,4	2	7
1,5	1	6
2,3	2	4,5
2,8	9	19
3,4	1	3,5
3,6	9	19
4,7	4	6,5
5,7	2	7
6,8	7	12
7,8	5	7,5

Решение находим с помощью сервиса Сетевая модель. В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная t_max(i,j) – при наиболее неблагоприятных условиях. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение t_ож(i,j) оценивается по формуле
t_ож(i,j)=(3 t_min(i,j)+2 t_max (i,j))/5
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=0,04(t_max(i,j)-t_min(i,j))2Рассчитаем ожидаемое значение и показатель дисперсии.
t_ож(1,2)=(3*5+2*10)/5=7
t_ож(1,4)=(3*2+2*7)/5=4
t_ож(1,5)=(3*1+2*6)/5=3
t_ож(2,3)=(3*2+2*4,5)/5=3
t_ож(2,8)=(3*9+2*19)/5=13
t_ож(3,4)=(3*1+2*3,5)/5=2
t_ож(3,6)=(3*9+2*19)/5=13
t_ож(4,7)=(3*4+2*6,5)/5=5
t_ож(5,7)=(3*2+2*7)/5=4
t_ож(6,8)=(3*7+2*12)/5=9
t_ож(7,8)=(3*5+2*7,5)/5=6
S2(1,2)=0,04*(10-5)2=1
S2(1,4)=0,04*(7-2)2=1
S2(1,5)=0,04*(6-1)2=1
S2(2,3)=0,04*(4,5-1)2=0,25
S2(2,8)=0,04*(19-9)2=4
S2(3,4)=0,04*(3,5-1)2=6,25
S2(3,6)=0,04*(19-9)2=4
S2(4,7)=0,04*(6,5-4)2=0,25
S2(5,7)=0,04*(7-2)2=1
S2(6,8)=0,04*(12-7)2=1
S2(7,8)=0,04*(7,5-5)2=0,25

Полученные данные занесем в таблицу.

Таблица – Сетевая модель.

Работа ( i,j)	Продолжительность	Ожидаемая продолжительность tож(i,j)	Дисперсия S2(i,j)
tmin (i,j)	tmax (i,j)
1,2	5	10	7	1
1,4	2	7	4	1
1,5	1	6	3	1
2,3	2	4,5	3	0,25
2,8	9	19	13	4
3,4	1	3,5	2	6,25
3,6	9	19	13	4
4,7	4	6,5	5	0,25
5,7	2	7	4	1
6,8	7	12	9	1
7,8	5	7,5	6	0,25

КПР	Код работы (i,j)	Продолжительность работы t(i, j)	Ранние сроки	Поздние сроки	Резервы времени
tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	Rп	Rc
1	2	3	4	5	6	7	8	9
1,2	7	7	7
1,4	4	4	17	21	17	8
1,5	3	3	19	22	19
1	2,3	3	7	10	7	10
1	2,8	13	7	20	19	32	12	12
1	3,4	2	10	12	19	21	9
1	3,6	13	10	23	10	23
2	4,7	5	12	17	21	26	9
1	5,7	4	3	7	22	26	19	10
1	6,8	9	23	32	23	32
2	7,8	6	17	23	26	32	9	9

_кр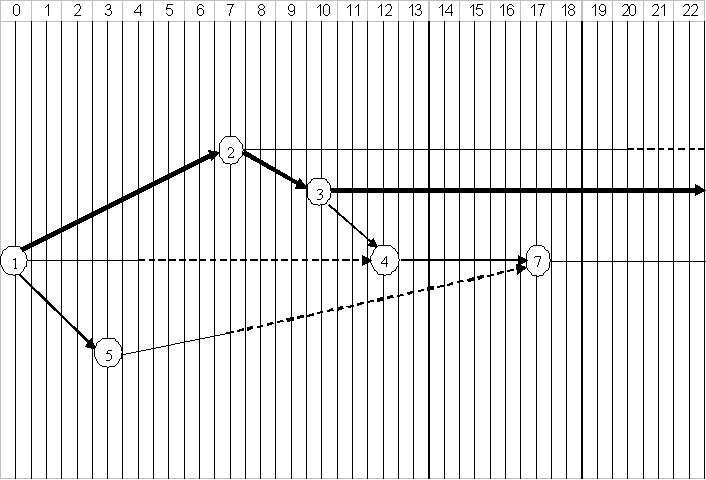

Рисунок — Масштабный график сетевой модели

P(t_кр
где Z=(Т-Т_кр)/S_крZ- нормативное отклонение случайной величины, S_кр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.
Соответствие между Z и Ф(Z) представлено в таблице.

Таблица — Таблица стандартного нормального распределения.

Z	F(Z)	Z	F(Z)	Z	F(Z)
0.0000	1.0	0.6827	2.0	0.9643
0.1	0.0797	1.1	0.7287	2.1	0.9722
0.2	0.1585	1.2	0.7699	2.2	0.9786
0.3	0.2358	1.3	0.8064	2.3	0.9836
0.4	0.3108	1.4	0.8385	2.4	0.9876
0.5	0.3829	1.5	0.8664	2.5	0.9907
0.6	0.4515	1.6	0.8904	2.6	0.9931
0.7	0.5161	1.7	0.9104	2.7	0.9949
0.8	0.5763	1.8	0.9281	2.8	0.9963
0.9	0.6319	1.9	0.9545	2.9	0.9973

Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8). 
Дисперсия критического пути:
S2­(L_кр)= S2(1,2)+ S2(2,3)+ S2(3,6)+S2(6,8)=1+0,25+4+1=6,25
S(L_кр)=2,5
p(t_кр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу:

T=Т_кр+Z*S_кр

Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z)  0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

Алгоритм построения сетевого графика

Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.

Шаг 1. Определить основную цель проекта

Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.

Шаг 2. Выявить ограничения

Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.

Шаг 4. Оценить длительность работ

Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.

Шаг 5. Определить последовательность работ

Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.

Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.

Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.

Шаг 6. Указать связи между работами

Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.

Шаг 7. Определить раннее начало и раннее окончание

Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.

Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.

Шаг 8. Определить поздние начало и окончание

Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Шаг 9. Определить временной резерв

Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Шаг 10. Выявить критический путь

Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.

Понятие «операция» в сетевом планировании

В сетевом графике можно оценить периоды начала (окончания) выполнения работ, вынужденные простои и, соответственно, максимальные сроки задержки производства тех или иных операций. Кроме того, выявляются критические операции – те, которые не могут выполняться с отклонением от графика.

Разбираясь с терминологией планирования, необходимо четко представлять себе, что такое операция. Чаще всего под этим понимают неделимую часть работ, требующую времени на выполнение. Далее мы понимаем, что с выполнением операции связаны затраты: времени и ресурсов (как трудовых, так и материальных).

В отдельных случаях для выполнения каких-то действий не нужны ресурсы, требуется только время, которое учитывает сетевой график. Пример этого — ожидание застывания бетона (в строительстве), время остывания прокатных деталей (металлургия) или же просто одобрение (подписание) контракта или разрешительной документации.

Чаще всего операциям в планировании дают наименование в повелительном наклонении (разработать спецификацию); иногда для названий используют отглагольные существительные (разработка спецификации).

Базовый алгоритм и виды связей сетевого графика

Сетевой график позволяет увидеть структуру работ, представить все этапы и взаимосвязи с требуемой степенью детализации. На его основе производится разработка обоснованного плана мероприятий с учетом более эффективного использования ресурсов по заданным критериям. Диаграмма позволяет производить поливариантный анализ альтернативных решений для улучшения календарного плана с использованием компьютерных технологий. Вспомним основные правила построения сетевой модели метода «вершина – работа».

1. Элементы сетевого графика включают работы и зависимости (связи) между ними. События на графике не отражаются за исключением вех, представляющих собой основные наиболее важные события, изображаемых в форме «ромбиков», работ с нулевой продолжительностью.
2. Работа представляет собой неделимый элемент процесса, требующий времени и других ресурсов для выполнения, изображается в виде прямоугольника, вытянутого по горизонтали. Исходя из этого правила, длина прямоугольника может свидетельствовать о продолжительности операции.
3. Разработка графика начинается с размещения на нем исходной работы в крайней левой точке и завершается включением в него конечной операции, закрывающей проект. Календарно начальный момент исходного действия обозначает старт проекта.
4. Зависимости (связи) между работами оформляются стрелками, направленными слева направо под разными углами наклона. На основе данного правила связи между операциями определяются одной из форм отношений зависимости.
5. Сетевой график имеет только одну работу, в которую входят зависимости, но не выходит ни одна, и одну работу, не имеющей ни одной входящей зависимости.
6. Сетевой график не может иметь циклов, т.е. зависимости не должны связывать работы по кругу.

Вид сетевого графика метода «вершина – работа»

Сетевой график строится по следующему алгоритму составления.

1. На диаграмме размещается начальная работа проекта, не имеющая предшественников.
2. Расположение операции, непосредственно следующей за работой, связанной с ней отношением предшествования, на графике левее предыдущей. Отображение связи предшествования.
3. Переход к пункту 2 до тех пор, пока не закончатся работы, имеющие предшественников.

Разработка сетевой диаграммы производится с учетом возможных связей между работами. Основные виды отношений предшествования используются в четырех вариантах связей и в двух дополнительных их разновидностях. Далее на схеме представлены варианты связи следующей по идентификационному номеру работы к предыдущей или, наоборот, последующей. Основные или базовые виды предшествования связаны с перестановками слов «начало» и «окончание»:

• «окончание – начало» (простой вид отношения предшествования);
• «окончание – окончание»;
• «начало – начало»;
• «начало – окончание».

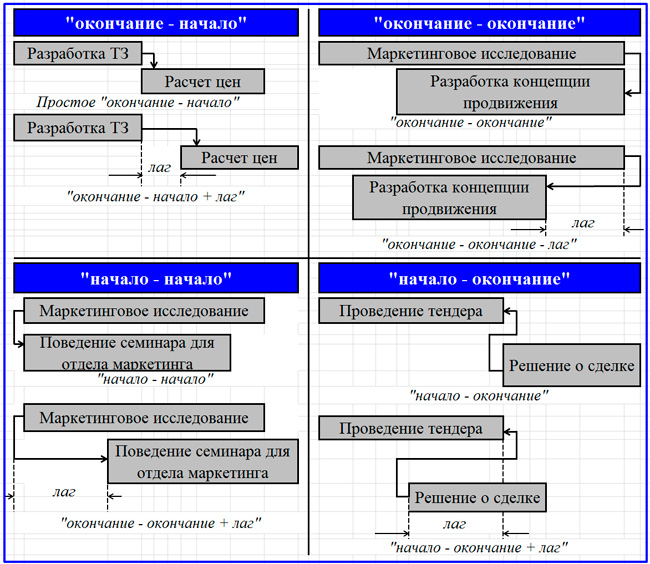Примеры вариантов отношений предшествования